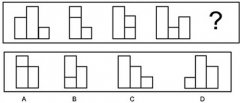
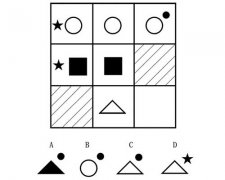
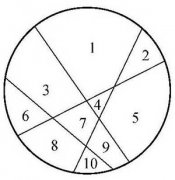
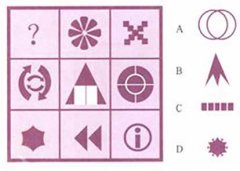
牛吃草问题经典例题

　　 牛吃草问题经典例题

逻辑思维题内容：

牛吃草问题经典例题，牛吃草一直是学生们最喜欢的经典案例题，深受大家喜爱，本文提供牛吃草问题经典例题及答案。

在伟大的物理学家牛顿的著作中有一本名著：一般算术。在这本书中有一道十分有名的题目：牛吃草问题。以下一起来看看两道牛吃草终极题！第一题牛吃草开胃题：假设一头牛一年可以吃掉4亩地的草，那么现在3头牛在一个20亩的牧场中，请问几年可以把草吃光?

牛吃草问题经典例题及答案：

吃不光，每年草都会长得。

二、有一片牧场的草，如果放牧27 头牛，则6个星期可以把草吃光;如果放牧23头牛，则9个星期可以把草吃光;如果放牧21头牛，问几个星期可以把草吃光?

iq智力题目提示：解答这道题时，我们假定牧草上的草各处一样密，草长得一样快，并且每头牛每星期的吃草量也相同。

牛吃草经典例题及解答：

在牧场上放牛，牛不仅要吃掉牧场上原有的草，还要吃掉牧场上新长出的草。因此解答这道题的关键，是要知道牧场上原有的牧草量和每星期草的生长量。

设每头牛每星期的吃草量为1。27 头牛6个星期的吃草量为27×6=162，这既包括牧场上原有的草，也包括6个星期长的草。23头牛9个星期的吃草量为23×9=207，这既包括牧场上原有的草，也包括9个星期长的草。 　　由于牧场上原有的草量一定，所以上面两式的差207-162=45 正好是9个星期生长的草量与6个星期生长的草量的差。由此可以求出每星期草的生长量是45÷(9-6)=15。

牧场上原有的草量是162-15×6=72，或207-15×9= 72。前面已假定每头牛每星期的吃草量为1，而每星期新长的草量为15，因此新长出的草可供15头牛吃。今要放牧21头牛，还余下21-5=6 头牛要吃牧场上原有的草，这牧场上原有的草量够6 头牛吃几个星期，就是21 头牛吃完牧场上草的时间。72÷6=十二(星期)。

也就是说，放牧21 头牛，十二个星期可以把牧场上的草吃光。

烧脑推理题：

三、同一条街上的2个店铺，共摆出100个土豆贩卖，一家店铺的土豆多，另一家店铺的土豆少，但他们却卖得了同样的钱。一家店铺boss对另一家店铺boss说："如果我有你那么多的土豆我能卖15元。"另一个说："如果我有你那么多的土豆，只能卖6元。"

你知道两家店铺各自有多少个土豆吗?

答案：一家店铺有40个土豆，另一家店铺有60个土豆。

更多相关推荐:
小学数学智力训练答案 小学生三年级趣味数学题（二十
培养幼儿数学逻辑思维题:A是多少
山东省考图形推理题之相同的咖啡杯